Tower of Hanoi Program in C using Recursion
Here you will learn the example code of Tower of Hanoi Program in C using Recursion.
What is Tower of Hanoi in Data Structures?
The Tower of Hanoi problem is a famous problem in computer science and mathematics that is often used to exemplify recursive algorithms and data structures. It consists of three pegs (rods) and a set of disks of different sizes, which can be stacked on the pegs. The goal of the problem is to move the complete stack of discs from one peg to another while according to the guidelines below:
- A single disc can only be moved at a time.
- A disc may only be placed on top of a bigger disc or an empty peg.
- A larger disk cannot be placed on top of a smaller disk.
The puzzle starts with all the disks on one peg, usually in decreasing order of size from bottom to top. The goal is to move all the disks to another peg, following the rules above, using the third peg as an auxiliary.
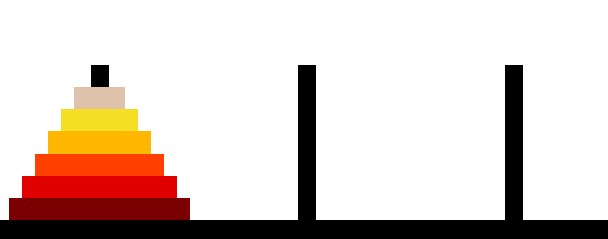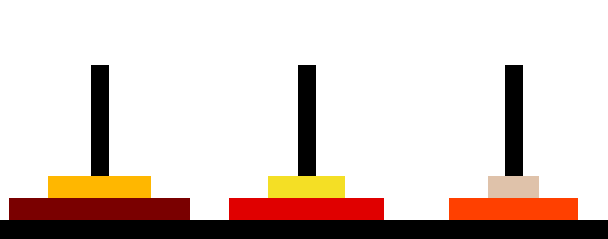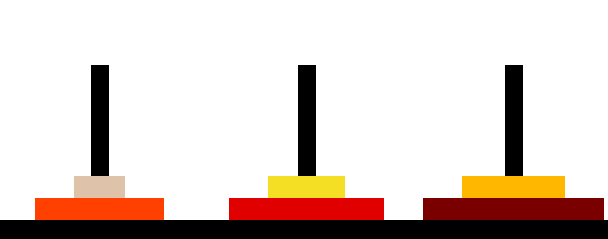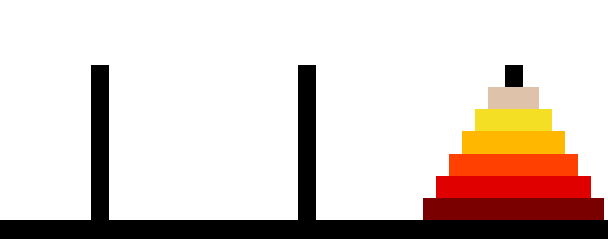
The following c program using recursion is given below to find the solution of Tower of Hanoi Problem.
Tower of Hanoi Program in C using Recursion
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | //Tower of Hanoi Program in C using Recursion #include <stdio.h> // Function to solve Tower of Hanoi problem void towerOfHanoi(int n, char source, char auxiliary, char destination) { if (n == 1) { printf("Move disk from %c to %c\n", source, destination); return; } towerOfHanoi(n - 1, source, destination, auxiliary); printf("Move disk from %c to %c\n", source, destination); towerOfHanoi(n - 1, auxiliary, source, destination); } int main() { int n; printf("Enter the number of disks: "); scanf("%d", &n); printf("Steps to solve the Tower of Hanoi problem with %d disks:\n", n); towerOfHanoi(n, 'A', 'B', 'C'); return 0; } |
Output
Enter the number of disks: 3
Steps to solve the Tower of Hanoi problem with 3 disks:
Move disk from A to C
Move disk from A to B
Move disk from C to B
Move disk from A to C
Move disk from B to A
Move disk from B to C
Move disk from A to C