Matrix Chain Multiplication in C
Here you will learn to program of matrix chain multiplication in c programming language.
Define Matrix Chain Multiplication
Matrix Chain Multiplication in c is a clever puzzle in Computer Science. Imagine having a list of matrices that need to be multiplied together. The trick is to figure out the best way to group them with parentheses, so you use the least number of multiplication steps. This puzzle pops up in designing efficient algorithms and gets solved using smart dynamic programming methods.
Let’s understand this problem using example
Input
1 | array[] = {10, 20, 30, 40} |
Output with Explanation
the matrices order will be
1 | Mat1 = 10X20, Mat2 = 20X30, Mat3 = 30X40 |
There are two methods to multiply these three matrices.
1 2 | mat1*(mat2*mat3) -> (10*20*40) + (20*30*40) = 8000 + 24000= 32000 (mat1*mat2)*mat3 -> (10*20*30) + (10*30*40) = 6000 + 12000 = 18000 |
In this example of (mat1*mat2)*mat3, the minimum number of multiplications is 18000
Dynamic programming optimizes matrix multiplication in C program by minimizing scalar multiplications.
Program of Matrix Chain Multiplication in C
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 | #include <stdio.h> #include <limits.h> int MatrixChainMultiplication(int dims[], int n) { int dp[n][n]; for (int i = 1; i < n; i++) { dp[i][i] = 0; } for (int len = 2; len < n; len++) { for (int i = 1; i < n - len + 1; i++) { int j = i + len - 1; dp[i][j] = INT_MAX; for (int k = i; k <= j - 1; k++) { int cost = dp[i][k] + dp[k + 1][j] + dims[i - 1] * dims[k] * dims[j]; if (cost < dp[i][j]) { dp[i][j] = cost; } } } } return dp[1][n - 1]; } int main() { int n,i,dims[20]; printf("Enter the value of matrices -> "); scanf("%d",&n); for(i=0;i<n;i++) { printf("Enter the [%d] value : ",i+1); scanf("%d",&dims[i]); } printf("Matrix Dimensions: {"); for (int i = 0; i < n; i++) { printf("%d", dims[i]); if (i < n - 1) { printf(", "); } } printf("}\n"); int result = MatrixChainMultiplication(dims, n); printf("Minimum number of scalar multiplications : %d\n", result); return 0; } |
Output
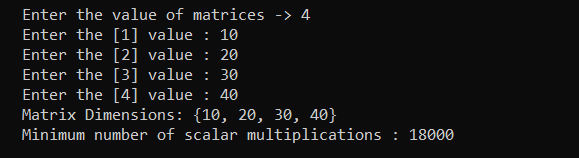
Read Also
Implement N Queens Problem using Backtracking
Knapsack Problem Using Greedy Solution
Perform Travelling Salesman Problem
Find Minimum Spanning Tree using Kruskal’s Algorithm